In this article we will look at parallel arrangement of resistors. We will also find out when to use this arrangement and how different electrical properties like resistance, voltage, current are affected.
Why combine resistors at all?
Combining resistors in certain ways produce a different equivalent resistance. For example: by using two 10K resistors and arranging them in parallel, you can obtain an effective resistance of 5K.
You might be wondering: When we can directly buy a resistor of any resistance value, why combine multiple resistors?
Well, generally the resistance of any resistor can vary from a few ohms to mega ohms. And it is not practically feasible to manufacture resistor for each possible resistance. So resistors with only a few standard resistance values are manufactured. And if we require a resistor with resistance anything other than the standard values, we need to combine multiple resistors with standard values in a certain way to get the desired resistance.
Two such types of resistor combinations are series combination of resistors and parallel combination of resistors. There can also be mixed combination of resistors with some groups of resistors connected in series and some others in parallel. In this article we will focus on parallel arrangement of resistors.
Parallel Combination of Resistors
Resistors are said to be in parallel with each other if one end of each of the resistors are connected at a single point and all the other ends are connected to another common point. Similar to the representation below:
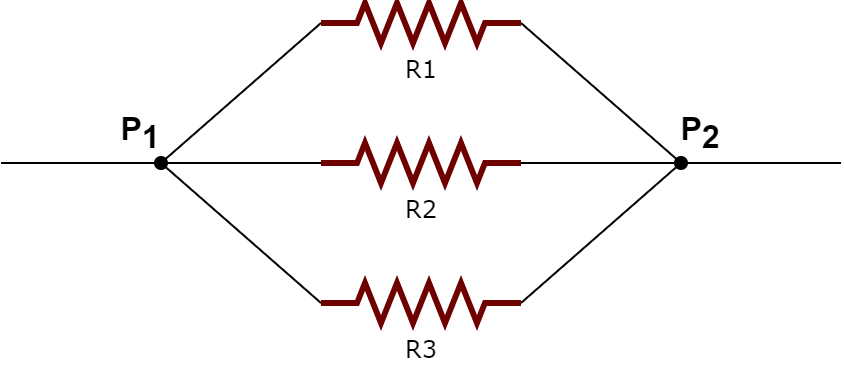
In the above combination of resistors, the left side terminals of resistors R1, R2 and R3 are connected to each other at a common point P1, and right side terminals of all the resistors are connected at a common point P2. Any number of resistors can be connected in this way and the whole arrangement can be said as resistors in parallel with each other.
Electrical Characteristics Resistors in Parallel

Let’s assume that the current coming out of power source is I amps. After reaching point P1, current has to split into 3 parts and flow through R1, R2, R3. After the current flows parallelly through all the resistors, it joins at point P2. If we denote the current passing through each of the resistors R1, R2, R3 as I1, I2, I3 respectively, the total current I should be equal to the sum of currents flowing through each of the resistors. So we have the below equation:
I = I1 + I2 + I3
Terminals towards left side of all the resistors are connected to a common point P1 and terminals towards right side of all the resistors are connected to a common point P2. Also the voltage between points P1 and P2 is equal to the supply voltage V. Hence the voltage across every resistor in parallel is same and is equal to the voltage across entire arrangement (V). So we have the below equation:
V = V1 = V2 = V3
Formula for Equivalent Resistance of Resistors Connected in Parallel
Let us derive the equation for the total effective resistance of all the resistors connected in parallel:
From the observation made in the previous section, we have:
I = I1 + I2 + I3 –> Equation 1
From Ohm’s law, voltage is equal to the product of current flowing through a resistor and the value of resistance (V = I * R). Rearranging the equation for I, we have:
I = V / R –> Equation 2
After assuming that the overall resistance of the entire parallel arrangement of resistors is R and substituting the current variables in equation 1 with the equation from ohm’s law, we have the following equation:
V / R = (V1 / R1) + (V2 / R2) + (V3 / R3)
But from observations in the previous section, we know that the voltage across any resistor connected in parallel is same as the overall voltage across all the resistors. So V1, V2, V3 can be substituted with V and the term can be cancelled on LHS and RHS sides. Finally we are left with the below equation:
1 / R = (1 / R1) + (1 / R2) + (1 / R3) and so on.
The same equation can be extended to any number of resistors connected in parallel. We just need to equate the reciprocal of overall resistance to the sum of reciprocals of all the resistors in parallel.
For example, if resistors 30K, 60K, 90K are in series, the equation will be 1/R = 1/30K + 1/60K + 1/90K. After taking LCM, and combining fractions, the equation becomes 1/R = 6/90K. Finally after inverting both LHS and RHS, we get R = 90K/6 = 15K (Note: Instead of writing: 1 Kilo Ohms, we used the short form: 1K)
TODO: Add a basic parallel resistor calculator for tinkering and some practical examples.
If you have any queries/suggestions, feel free to post them in the comments section of this video: Resistors In Parallel